Um die Kurve gedacht: Wie wir Millionen von Verspätungsdaten übersichtlich aufbereiten
Seit Monaten sammeln wir Verspätungsdaten: aktuell ca. 9 Millionen Datenpunkte, vor allem aus dem Verkehrsverbund Bremen Niedersachsen. Das ist natürlich kein Selbstzweck.
Aus den vergangenen Verspätungsdaten möchten wir Statistiken erstellen, und daraus Prognosen für die nahe Zukunft. Und damit letztlich unserer Routensuche die bestmöglichen Ergebnisse liefern.
Jetzt haben wir erste statistische Analysen und ein paar bunte Bilder dazu. Was sieht man darin, wie sind sie entstanden, und wofür sind sie gut?
(Bilder anklicken, um sie zu vergrößern. Hovern für eine Kurzbeschreibung.)
Bereits in unserem vorletzen Post schrieben wir, dass wir von den Verkehrsbetrieben “nur” Prognosen bekommen. Die haben wir zunächst auf Echtzeitdaten herunter gebrochen, gesammelt, und nun machen wir daraus wieder eigene Prognosen. Wozu so viel Aufwand?
Klassische Prognosen
Zunächst muss man mal betrachten, was die Verkehrsbetriebe unter Prognosen verstehen. Für ein bestimmtes Fahrzeug wird vorhergesagt, wann es an einer bestimmten Haltestelle ankommen oder abfahren wird. Dabei wird die planmäßige Zeit um eine Anzahl von Sekunden vor- oder zurückverlegt. Das Ergebnis ist also ein Zeitpunkt. Für jedes Fahrzeug erhalten wir minütlich Prognosen für seine Ankunft an den nächsten 5 bis 10 Haltestellen.
Der prognostizierte Zeitpunkt wird meist mit “sekundengenau” angegeben - wobei es auffällige Häufungen bestimmter Werte gibt, die am Ende des Artikels nochmal betrachtet werden. So oder so handelt sich um jeweils eine einzige, quasi alternativlose Prognose - so als könnte man mit Sicherheit sagen, wie viel Verspätung ein Verkehrsmittel in Zukunft haben wird. Dabei ist die Existenz von Verspätungen doch selbst schon Beweis dafür, dass ÖPNV nicht deterministisch einem Plan folgt. Zudem wird jede Prognose ja minütlich durch eine - ggf. unterschiedliche - neue Prognose ersetzt. Realistisch betrachtet müsste jede Prognose natürlich mit irgendeiner Form von Unsicherheit behaftet sein, aber in den Daten ist diese nicht zu finden.
Im quasi-Standard GTFS-Realtime (den in Deutschland längst nicht alle Verkehrsbetriebe unterstützen) ist sogar ein Datenfeld vorgesehen, um Unsicherheiten von Prognosen auszudrücken - dessen statistische Bedeutung aber explizit undefiniert ist und das weltweit kaum ein Datenanbieter nutzt. Also haben wir unsere eigene Defition für Unsicherheit geschaffen.
In diesem Blogpost soll es also darum gehen, was wir definiert haben, und wie bzw. warum wir das getan haben. Und letztlich auch um die Erkenntnisse, die dabei aufgetreten sind.
Zweck unserer Analysen und Prognosen
Eine zentrale Fragestellung innerhalb unserer Routenberechnungen ist, ob ein Anschluss erreicht wird, oder genauer gesagt: mit welcher Wahrscheinlichkeit er erreicht wird, und wenn ja, wann das wohl sein wird. Ein Anschluss kommt dann zustande, wenn das erste Fahrzeug ankommt, bevor das zweite abfährt, und der Zeitabstand größer ist als die Zeit, die zum Umstieg gebraucht wird.
Dazu brauchen wir für beide Fahrzeuge eine Prognose für die Ankuft bzw. Abfahrt an der Umsteigehaltestelle. Erfahrungen mit unserem ersten Prototyp aus dem August 2019 haben gezeigt, dass wir für eine einzelne Routenabfrage oft viele Tausende solcher Prognosen brauchen. Damals hatten wir eine mittelgroße Datensammlung aus hunderttausenden Verspätungen auf wenige hunderte Bytes herunter gebrochen, die in Form von Arrays und Maps direkt im Quelltext standen. Damit konnten wir Prognosen innerhalb von Mikrosekunden berechnen, ohne auf Datenbanken, Netzwerkdienste oder externe Dateien zurück zu greifen. Entsprechend grob, realitätsfern und frei von aktuellem Kontext waren die Prognosen aber auch.
Diesmal gilt es, einen guten Kompromiss zu finden: Wie können wir in unsere Prognosen möglichst viele Details unserer 1,7 GB gesammelten Daten einfließen lassen, ohne dafür ebensoviele Daten im RAM vorzuhalten und sie immer wieder aufs neue durchzuarbeiten? Können wir die Essenz der Daten mathematisch fassen, verlustarm komprimieren und so ablegen, dass wir effizient Abfragen darauf durchführen können?
Natürlich haben wir etwas recherchiert, ob es bereits bewährte Methoden dazu gibt, jedoch ohne nennenswerten Erfolg. Vielleicht fehlen uns die Fachkenntnisse in multivariater Statistik, um das richtige Verfahren aus den vorhandenen zu erkennen, dafür sind wir in genug anderen Bereichen der Informatik bewandert, um eine eigene Lösung zu entwickeln und dabei nicht bei Null zu beginnen.
Darstellung von (Wahrscheinlichkeits-)Verteilungen
Histogramme sind ein bewährtes Werkzeug zur Darstellung von Verteilungen - die meisten kennen es vermutlich aus der Bildbearbeitung, wo sie die Verteilung der Helligkeitswerte von Pixeln anzeigen.
Wir verwenden für Dystonse eine artverwandte Darstellung, nämlich die Summenhäufigkeit. Dabei speichern wir für die einzelnen Verspätungswerte nicht, wie oft genau dieser Wert auftritt, sondern welcher Anteil der Verspätungen höchstens diesen Wert hat. Das hat vielfältige Vorteile:
- Für die oben genannte zentrale Fragestellung - kommt Fahrzeug A an, bevor Fahrzeug B abfährt? - können wir Werte direkt als Summenhäufigkeit ablesen, anstatt immer wieder Einzelhäufigkeiten aufzuaddieren.
- Die Darstellung als Summenhäufigkeit ist unabhängig von der Auflösung. Da Verspätung eine kontinuierliche Größe ist, tritt praktisch nie zweimal die selbe Verspätung auf. Eine histogrammartige Darstellung entsteht nur, wenn die Verspätungen in Klassen eingeteilt werden, wie z.B. “zwischen 2 und 3 Minuten”. Die Höhe der Peaks ist dann von der Breite dieser Klassen abhängig und ihr Wert ist ohne Angabe der Breite nicht aussagekräftig.
- Histogramme sind anfälliger für Artefakte durch Messungenauigkeiten und Rundungen - somit aber auch besser geeignet, um diese aufzudecken.
- Die Kurve der Summenhäufigkeit lässt sich effizienter komprimieren, bzw. zwangsläufig auftretende Fehler durch die Datenreduktion wirken sich kaum auf das effektive Ergebnis aus.
- Die Darstellung der Summenhäufigkeiten ist übersichtlicher, da die Kurven sich weniger oft kreuzen.
Hier ist eine Gegenüberstellung der beiden Darstellungsweisen, zunächst ähnlich einem Histogramm:
(Bilder anklicken, um sie zu vergrößern)
Im Histogramm ist auf die Schnelle kaum etwas zu erkennen und der Wert auf der y-Achse hat für sich genommen keine Aussagekraft. Die selben Daten in aufsummierter Darstellung:
(Bilder anklicken, um sie zu vergrößern)
Als Summenhäufigkeit dargestellt, sind die gleichen Daten deutlich leichter zu überblicken, denn die Kurven kreuzen sich prinzipbedingt kaum. Allerdings ist die Darstellung für viele Menschen auch ungewohnter und nicht auf den ersten Blick verständlich.
Nach etwas Ein- bzw. Umgewöhnung sind hier wichtige, aussagekräftige Werte direkt ablesbar, wie z.B. “Wie viel Prozent der Fahrten sind höchstens 60s verspätet” oder “Welche Verspätung wird nur in 5% der Fahrten überschritten?”. Das ist nicht nur eine Vereinfachung für den Menschen, der mit bloßem Augen einen Wert aus einer Grafik abliest. Auch für den Computer, der später genau diese Fragen beantworten muss, ist es effizienter, einen Wert auf der Kurve zu bestimmen, als immer wieder das Integral über einen Teil der Kurve zu bilden. Letztlich lassen sich die Summenkurven für uns besser komprimieren als das äquivalente Histogramm.
Die Vorteile dieser Darstellung bzw. Speicherung überwiegen also deutlich - im weiteren Verlauf dieses Textes, sowie auch in später folgenden Blogposts, verwenden wir daher nur noch aufsummierte Häufigkeiten.
Verarbeitung, Vereinfachung und Speicherung
Um diese Kurven effizient und vielseitig einsetzen zu können, haben wir das Rust-Paket dystonse-curves angelegt. Damit können wir Summenhäufigkeiten in verschiedene Datenstrukturen verpacken, die sich über ein einheitliches Interface ansprechen lassen, das die wichtigsten Operationen darauf bereitstellt. Das Herzstück für die Speicherung ist die IrregularDynamicCurve, die eine Kurve anhand von geordneten XY-Paaren darstellt. Da alle Kurven monoton steigend sind, können Anfragen sowohl nach X- als auch nach Y-Werten effizient per binärer Suche erfolgen. Und da die Punkte ungleichmäßig verteilt sein können, und veränderbar sind, können wir diese Kurven reduzieren, indem wir Punkte entfernen, die sich auf die Gesamtform nur unwesentlich auswirken.
Um diese Reduktion zu erreichen, verwenden wir den Ramer-Douglas-Peucker-Algorithmus, der vor allem in der Computergrafik und Geoinformatik populär ist. In der Praxis können wir damit unsere Kurven, die anfangs aus 25 bis 1200 Punkten bestehen, meist auf 5 bis 12 Punkte reduzieren. Außerdem genügt uns theoretisch jeweils ein Byte zur Speicherung einer Koordinate, denn unsere Daten sind niemals so genau, dass sie unbrauchbar würden, wenn sie sich um 1/256 verändern.
(Bilder anklicken, um sie zu vergrößern)
Auf unserem Server herrscht noch keine Speicherknappheit, doch werden wir später einmal derartige Verteilungskurven an Mobilgeräte senden müssen, die sich außerdem oft in Bereichen mit schlechtem Mobilfunkempfang befinden. Eine Reduktion der Daten ist also besonders wichtig. Binär kodiert können wir eine komplette Wahrscheinlichkeitsverteilung in ca. 20 Byte verpacken - eine einzelne Fließkommazahl in JSON-typischer Darstellung mit Schlüssel und Wert hat etwa den selben Umfang.
Anwendung auf unsere Problemstellung
Im ersten Schritt unserer Analyse betrachten wir für einen Linienverlauf jedes Paar aus Start- und Zielhaltestelle, und untersuchen den Zusammenhang zwischen der Verspätung am Start und am Ziel. Dazu suchen wir in unseren Aufzeichnungen von Fahrten, bei denen wir für beide Haltestellen Verspätungswerte haben.
Im folgenden Beispiel gibt es 402 solcher Fahrten. Die folgende Grafik enthält für Start und Ziel jeweils die Verteilung der Verspätungen, und für 35 zufällige der 402 Wertepaare haben wir den den Punkt für die Anfsangsverspätung und die Endverspätung mit einer Strecke verbunden.
Nun wollen wir aber nicht nur wissen, wie Verspätungen am Ziel allgemein verteilt sind, sondern wie sie für eine bestimmte, bekannte Anfangsverspätung verteilt wären.
Klassifizierung der Datenpunkte
Um den Zusammenhang der beiden Größen zu bestimmen, teilen wir unsere Datenpunkte in Klassen verschiedener Start-Verspätungen ein, denn wir müssen stets eine Menge von Einzelbeobachtungen zusammen fassen, um eine (näherungsweise) Verteilung zu ermitteln.
Die Aufteilung ist aber nicht trivial. Teilt man die Datenpunkte gleichmäßig nach Anzahl der Datenpunkte ein, so decken diese Klassen sehr unterschiedliche Spannen von Anfangsverspätungen ab. Im Folgenden Bild wurden die 402 Datenpunkte in Klassen zu je 50 bzw. 51 Punkten eingeteilt, wobei die vorletze Klasse Verspätungen von 36s bis 48s abdeckt, die letzte hingegen alle Daten von 48s bis 432s zusammen wirft. Die Aufteilung ist also an manchen Stellen (zu) fein, an anderen zu grob.
Wenn wir stattdessen gleich “breite” Klassen wählen (z.B. je 10 Sekunden, also von -70s bis -60s, von -60s bis -50s, usw.) so sind die Klassen sehr unterschiedlich stark gefüllt. Oft liegen eine einstellige Anzahl von Datenpunkten oder sogar gar keine Punkte in den Extremen, dafür hunderte Punkte in der Klasse um 0s herum. (Hierzu gibt es keine Grafik.)
Wir haben daher ein rekursives Verfahren entwickelt, das zunächst alle Daten als eine Klasse ansieht und prüft, ob und wie diese in zwei Unterklassen eingeteilt werden kann. Wenn dies geschieht, wird für jede der Unterklassen die gleiche Prüfung und ggf. Teilung wiederholt. Dabei muss jede neue Klasse sowohl eine Mindestmenge an Datenpunkten enthalten, als auch eine Mindestbreite an Anfangsverspätungen abdecken. Für die gegebene Verteilung von Anfangsverspätung erhalten wir diese Aufteilung:
Eine weitere Verfeinerung unseres Ansatzes besteht darin, dass wir nicht mehr alle Datenpunkte einer Klasse stumpf zusammen werfen (also etwa alle Fahrten mit einer Anfangsverspätung zwischen 135s und 432s gleich behandeln), sondern gewichtet aufsummieren. Im gegebenen Beispiel würden wir also eine Kurve für alle Fahrten erstellen, die “ungefähr 135s” verspätet beginnen, und eine andere Kurve für alle Fahrten, die “ungefähr 432s” verspätet sind.
Eine Fahrt mit 170s Anfangsverspätung (in der nächsten Grafik grün hervorgehoben) würde mit sehr hoher Gewichtung in die erste Kurve eingehen, und nur mit einer sehr geringen Gewichtung in die zweite. Dabei bestimmt die Anfangsverspätung, wie sehr der Datensatz in die jeweilige Summe eingeht, aber die Endverspätung, was aufsummiert wird, und jeder Datensatz geht in ein oder zwei Summenkurven ein:
Für unsere sieben Klassengrenzen ergeben sich damit sieben Ergebniskurven, die den Zusammenhang zwischen Anfangs- und Endverspätung viel genauer wiedergeben können, als es eine einzelne Verteilungskurve könnte. Die Zahl in Klammern ist dabei ein Indiz für die Menge der Datenpunkte, die aufsummiert wurden, so besteht die 432s-Kurve aus (mehr als 14) Datenpunkten mit einem Gesamtgewicht von 14.05.
Überblick über riesige Datenmengen
Wir haben bis jetzt 9.094.120 Datenpunkte aufgezeichnet.
Viele unserer Beobachtungen haben wir anhand der Straßenbahnlinie 4 in Bremen durchgeführt. Zuerst war das eher eine zufällige Auswahl, da unsere Mitbewohnerin uns nach Beispielen dieser Linie fragte, die sie aus ihrer Jugend kennt. Erst später haben wir gemerkt, dass dies tatsächlich eine der Linien mit der besten Datenlage ist: aktuell haben wir davon 220.365 Datenpunkte.
Jede Linie hat mehrere Varianten - im Fall der Linie 4 sind das 11 Varianten, was ein völlig typischer Wert ist. Und für jede Variante erzeugen wir eine Grafik für jedes Haltestellenpaar, das sind z.B. für eine Linienvariante mit 36 Haltestellen dann 161 Grafiken mit je ca. 2 bis 10 Ergebniskurven. So kommen sehr schnell zehntausende Grafiken zusammen. Wie schnell? Im Schnitt können wir alle 68ms eine neue generieren, und nutzen dabei derzeit nur ein Viertel unserer CPU-Kerne.
Wir haben einige Stunden damit verbracht, diese nach Fehlern, Auffälligkeiten und Kuriositäten zu durchsuchen. Um aber einen besseren Überblick über unsere Datenqualität zu erlangen, waren auch Übersichtsgrafiken wie die folgenden sehr wertvoll. (Es handelt sich um zwei der vier Grafiken, die schon zu Beginn des Textes ganz klein als Teaser-Bilder herhalten mussten.)
So zeigt sich hier, dass die Tram 4 vorallem in der Mitte der Strecke dazu neigt, Verspätungen von 1-2 Minuten zu haben (blau-grünliche Kurven), und dann gegen Ende (dunkelrote Kurven) auch gerne mal bis zu 2 Minuten zu früh abfährt:
Die gleichen Folgerungen lassen sich auch diesen drei Ansichten ableiten:
(Bilder anklicken, um sie zu vergrößern)
An eine Darstellung als Boxplot hatten wir zunächst gar nicht gedacht, und haben sie auch nicht vermisst, da wir uns daran gewöhnt hatten, die Daten aus Kurven heraus zu lesen. Nachdem die erste Fassung dieses Blogposts online ging, haben wir einen Hinweis dazu erhalten, und die Darstellung noch hinzu gefügt. Wenn man genau hinsieht, merkt mann, dass im Grunde genommen der gleiche Verlauf wie in den Kurven der vorherigen Grafik gezeichnet wird.
Erkenntnisse
Die allererste Feststellung: die Kurven aus unseren gesammelten Daten sehen tatsächlich etwa so aus wie das, was wir uns in den Monaten zuvor vorgestellt haben, und was sich in unseren Bleistiftskizzen vielfach wieder findet.
Und es bestätigen sich weitere Vermutungen und offensichtliche Zusammenhänge:
- Fahrten, die zu Beginn schon mehr Verspätung haben, haben tendentiell auch am Ende noch mehr Verspätung.
- Negative Verspätungen - also eigentlich Verfrühungen - kommen zwar vor, aber seltener und in kleinerem Ausmaß als positive Verspätungen. Überhaupt betreffen sie viel öfter die Ankunft an einem Halt, als die Abfahrt, d.h. das Fahrzeug bleibt i.d.R. länger stehen, wenn es “zu früh” angekommen ist.
- Es gibt eine klare Häufung um 0s herum, d.h. dass ein Fahrzeug ungefähr pünktlich ist, ist der häufigste Fall
- Straßenbahnen sind pünktlicher als Busse (dabei haben wir aber bisher nur 2 Bus- und 2 Tramlinien genauer betrachtet)
- Manche Linienabschnitte fügen tendenziell mehr Verspätung hinzu, andere erlauben eher, Verspätungen wieder auszugleichen
Weniger erwartet hatten wir die folgenden Erkenntnisse:
- Je nach Haltestelle schwankt die Verfügbarkeit und Qualität von Echtzeitdaten enorm, selbst wenn diese eigentlich von gleich vielen Fahrzeugen passiert werden. Es scheint, als würden manche Haltestellen bzw. Streckenzüge über 2-4 Haltestellen hinweg in einer Art “Funkloch” liegen.
- Es gibt einige Ausreißer mit Verspätungen in der Größenordnung von -3600 oder +3600 Sekuden, also einer ganzen Stunde. Für unsere Auswertungen schließen wir derzeit alle Abweichungen von mehr als 3000 Sekunden (also 50 Minuten) komplett aus. Zudem schneiden wir die Darstellung der Diagramme bei 450 Sekunden ab, um den interessanten Kernbereich besser sichtbar zu machen.
- Manchmal finden sich in den Kurven interessante Muster und Unregelmäßigkeiten, die dennoch plausibel sein können. Im folgenden Beispiel finden sich einige Stufen / Schultern / Sattelpunkte im Abstand von 90s in den Kurven. Da liegt die Vermutung nahe, dass sich kurz vor der Haltestelle eine Ampel befindet, an der ein Bus warten muss, bevor er den Halt erreicht. Wir haben das auf der Straßenkarte geprüft, und tatsächlich muss der Bus dort an einer Ampel warten, direkt bevor er an der Haltestelle hält. Ob die Ampeln dort wirklich einen 90-Sekunden-Zyklus haben, konnten wir aus der Ferne jedoch nicht heraus finden.
(Bus Linie 21 in Bremen, Verspätung an der Haltestelle “Horn”: Hier sind einige auffällige Stufen erkennbar, die jeweils ca. 90 Sekunden breit sind. Der Bus kommt von Norden und hält dann südlich der Kreuzung am Bussteig.)
(Im Kartenausschnitt ist die Ampel markiert, die vermutlich für die Stufen im obigen Diagramm verantwortlich ist.)
Rundung
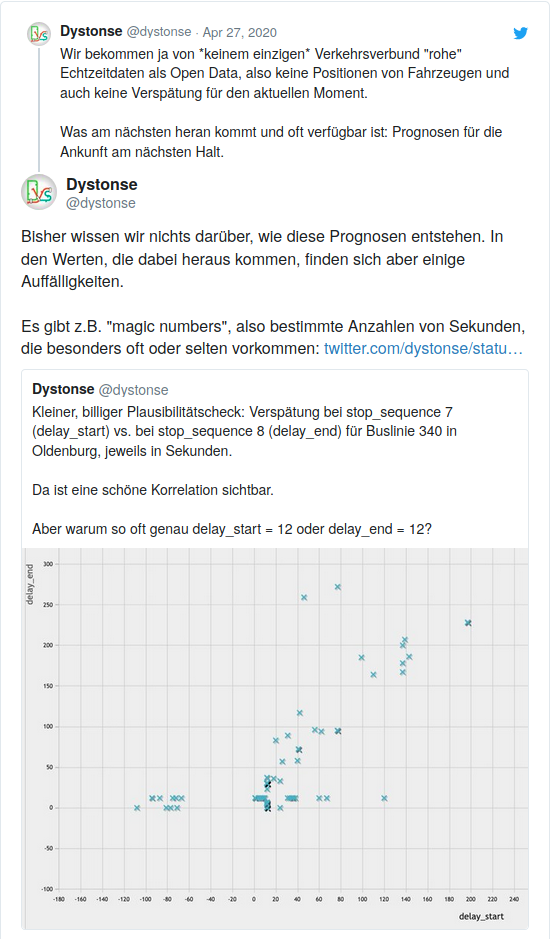
Schon im April sind uns Ungereimtheiten in den Daten aufgefallen, und wer uns auf Twitter folgt, hat das vielleicht schon mitbekommen:
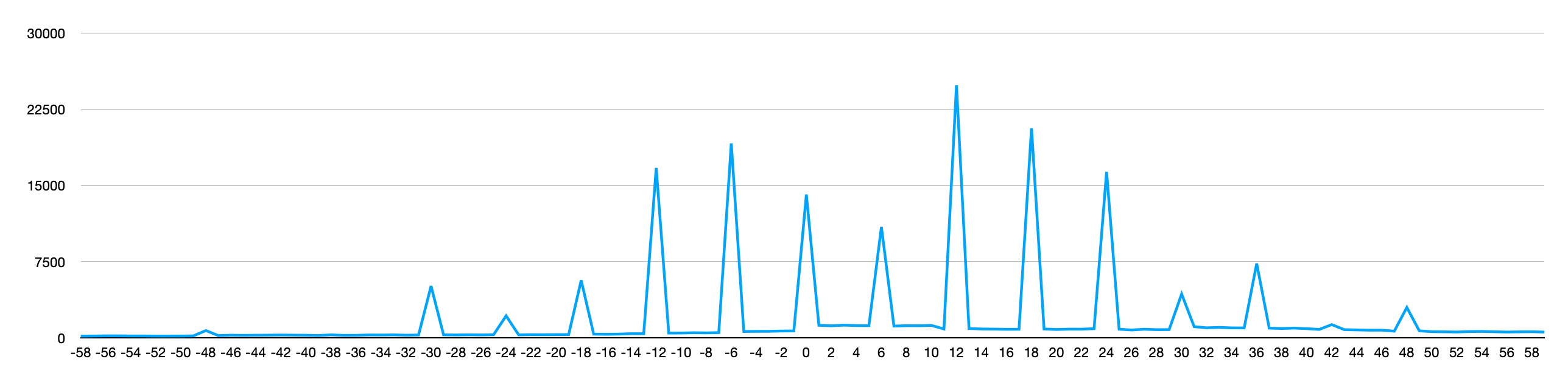
Ein Großteil der Daten wurde also vom Anbieter auf ganze Vielfache von 6 oder gar 12 Sekunden gerundet, aber es gibt stets auch Daten, die “krumme” Werte enthalten. Hier die Verteilung der Verspätungen modulo 60:
Die Rundung hat zu sichtbaren Verzerrungen unserer Grafiken geführt, die oft die eigentliche Essenz der Information überdeckt haben. Da wir nicht davon ausgehen, dass Prognosen genauer als 12s aufgelöst sein müssen, bzw. dass eine höhere Auflösung praxisrelevant wäre, runden wir nun alle Daten vor der Verarbeitung auf 12 Sekunden.
Nächste Schritte
Derzeit können wir diese Kurven nur als Grafiken ausgeben. (Wir nutzen hier SVG, aber PNG, PDF, etc. funktionieren ebenso). Natürlich brauchen wir für die Praxis eine kompakte, effizient maschinenlesbare Form und eine Weise, die Kurven für sämtliche Haltestellenpaare aller Linien abzulegen und wiederzufinden.
Später möchten wir noch weitere Einflussgrößen betrachten und danach getrennte Kurven ermitteln, wie z.B. Wochentag und Uhrzeit. So soll für jede gültige Kombination aus den folgenden Eingabegrößen eine Verteilung ermittelt werden können:
- Linie und Linienvariante
- Tag
- Uhrzeit
- Start-Haltestelle (für die eine aktuelle Verpätung bekannt ist)
- Wert der aktuellen Verspätung
- Ziel-Haltestelle (für die die Verteilung von künftigen Verspätungen gefragt ist)
Und wir brauchen einen Algorithmus (sowie eine Schnittstelle, Infrastruktur, etc.) um daraus tatsächlich Prognosen zu erstellen. Dazu werden wir die aktuelle Verspätung jedes Fahrzeugs nutzen, um die passende(n) Kurve(n) aus unserer Analyse zu laden und mittels Sampling und Interpolation Verteilungen für den weiteren Fahrtverlauf zu prognostizieren.
Diese Prognosen werden wir für unseren eigenen Suchalgorithmus einsetzen, aber wir möchten sie auch für andere Projekte verfügbar machen. Das naheliegende Format GTFS-Realtime ist dafür, wie oben schon angedeutet, noch nicht ausreichend detailiert. Derzeit beteiligen wir uns an einer Diskussion mit weiteren Entwickler_innen, die sich ebenfalls eine solche Erweiterung des Standards wünschen.
Die Analysen und Grafiken wurden mit unserem Paket dystonse-gtfs-data erzeugt. Die Grafiken im Abschnitt ‘Klassifizierung der Datenpunkte’ wurden zudem mit Inkscape bearbeitet, um die Erläuterungen einzufügen.
Aktuell strukturieren wir den Code um, damit Analyse und Grafikausgabe besser getrennt sind. Die neueste Revision kann nicht alle hier gezeigten Arten von Grafiken erzeugen. Der letzte Commit, mit dem das noch geht, ist dieser. Wir denken, dass künftige Versionen wieder alle Grafiktypen erzeugen können werden, aber das ist aktuell nicht die oberste Priorität unserer Entwicklung.